GRADO UNDÉCIMO - APOYO GEOMETRÍA UNO

 

DISEÑO INSTITUCIONAL ACTIVIDADES VIRTUALES

 

SEDE: PRINCIPAL JORNADA: MAÑANA CURSO: UNDÉCIMO FECHA: 30 SEPTIEMBRE 2020

DIMENSIÓN/AREA/ASIGNATURA/MODULO: INFORMÁTICA

NOMBRE DEL DOCENTE: EUSEBIO PRADA MATIZ

NOMBRE DE LA ACTIVIDAD GENERAL: APOYO EN GEOMETRÍA PARA LAS PRUEBAS SABER

TIEMPO TOTAL: 2 HORAS

MOMENTO INICIAL

EXPLICACIÓN DE LA ACTIVIDAD GENERAL: Revisión de conceptos de Geometría a través de una prueba tipo saber.

IMÁGENES RELACIONADAS CON LA TEMÁTICA

Recordemos un poquito de Geometría Si buscamos en Google la definición de Geometría, seguramente encontraremos, que es un nombre femenino, cuya definición es: “Parte de las matemáticas que estudia la extensión, la forma de medirla, las relaciones entre puntos, líneas, ángulos, planos y figuras, y la manera cómo se miden.” Todo este maravilloso mundo arranca con el elemento más básico: el punto y de ahí en adelante vienen un cúmulo de conceptos que hace que las personas que los conozcan vean el mundo de otra manera. El punto, la recta y el plano son los elementos fundamentales de la geometría y ellos tres han ayudado a poner las bases para áreas como las ciencias naturales, las ciencias sociales, la tecnología, pero sobre todo en la vida diaria. Así que los invito a que recordemos algunos conceptos a través de estas preguntas. 1.      La pendiente de una recta en el plano cartesiano, es un concepto intuitivo de la vida diaria, y podemos decir que es el ángulo de inclinación que registra dicha línea con respecto al eje X. El punto de corte o intersección con el eje Y, es el punto donde se cruza la citada línea o su prolongación con dicho eje. (Imagen 1.) 1. Podemos afirmar que dos rectas son paralelas en un plano cartesiano si se encuentra que sus pendientes son iguales y el punto de corte con el eje Y de cada una de ellas es diferente. Este enunciado final es: A.      Verdadero B.      Falso C.      Verdadero algunas veces D.     Falso casi siempre        2.      Se dice que dos rectas son perpendiculares u ortogonales, si al cruzarse o cortarse se forman ángulos de 90° (rectos) entre ellas. Un ejemplo de esto, es el plano cartesiano, en el cual se cruzan los ejes X y Y, formándose ángulos de 90° entre ellas (Imagen 2.) Son ejemplos de esta situación, las líneas: A.      que forman un ángulo agudo B.      que forman un ángulo obtuso C.      de una columna y una fila en Excel D.     opuestas de un cuadrado       3.      Si dos líneas paralelas son cortadas por una tercera de forma oblicua se forman ocho ángulos, cuatro por cada corte. De la imagen correspondiente (Imagen 3.) se puede decir que NO es verdad: A.      < A + < B = 180° B.      < E = < G C.      < F + < G = 180° D.     < B = < C 4    4.      Los ángulos se pueden sumar, gráfica y analíticamente. La imagen 4 ilustra la forma gráfica. Si se tiene el valor en grados de dos ángulos se hace una suma con dichos valores. Ej. Un ángulo de 30 ° + un ángulo de 45° = un ángulo de 75°.          La suma de dos ángulos rectos es igual a un ángulo llano. De lo anterior se puede afirmar que un ángulo llano mide: A.      45° B.      90° C.      135° D.     180°       5.      Del enunciado anterior y la imagen 3 podemos decir que el ángulo A = ángulo C, porque, <A + < B = 180° y <B + <C = 180° Entonces: <A + <B = <B + <C, si en cada lado de la ecuación quitamos el <B Tenemos que: <A = <C Podemos decir entonces que: A.      <A = <D B.      <B = <C C.      <B = <D D.     <C = <D      6.      Un rectángulo es una figura geométrica que tiene 4 lados: 2 largos y 2 cortos. Sus lados opuestos son paralelos y los cuatro ángulos internos son ángulos rectos. Esto último quiere decir que dos lados consecutivos (uno largo y uno corto) son perpendiculares u ortogonales. Cuántos rectángulos se ven en la figura 5. A.      7 B.      10 C.      12 D.     Más de15        7.      La suma de los ángulos internos de un rectángulo, es igual a: A.      90° B.      180° C.      360° D.     450°     8.      El triángulo, el rectángulo, el cuadrado, entre muchos otros, son polígonos, o figuras geométricas planas que están limitadas, es decir, cerradas por 3 o más lados. En la imagen 6, se trazaron las diagonales del cuadrado. ¿Cuántos triángulos se formaron? A.      4 B.      8 C.      12 D.     16        9.      Para calcular el número de diagonales de un polígono, se aplica la fórmula: n(n-3) /2, para el caso del cuadrado se tiene: Numero de diagonales = 4(4-3) / 2 Número de diagonales = (16 – 12) / 2 Número de diagonales = 4 / 2 Número de diagonales = 2 (ver imagen 6) ¿Cuántas diagonales tiene un octágono o polígono de 8 lados? A.      20 B.      16 C.      12 D.     8      10.  Teniendo en cuenta que vértice es el punto en donde se unen dos lados consecutivos de un polígono, y que un polígono regular es aquel que tiene todos sus lados y sus ángulos iguales. La definición de diagonal en un polígono regular más acertada es: A.      Una línea en un polígono que de forma recta une los vértices B.      Una línea interna en un polígono que forma ángulo recto con los vértices C.      Cualquier segmento de recta que una los vértices de un polígono interno D.     Segmento de línea recta que une internamente dos vértices no consecutivos en un polígono      11.  El punto es quizá el concepto o elemento fundamental, básico de la geometría, porque sirve para definir o producir el concepto de línea y de plano. Suele también decirse de él que es la intersección de dos líneas. Indica una posición, por ejemplo, el inicio o el final de una línea. Se dice que es adimensional, es decir que no tiene ancho, largo o alto, aunque se marque geométricamente. Un milímetro cuadrado es la millonésima parte de un metro cuadrado. Se escribe 1 mm2 = 0,000001 m2. Se puede decir que en un milímetro cuadrado caben: A.      Millones de puntos B.      Infinitos puntos C.      Algunos puntos D.     Muchos puntos       12.  La idea de punto se desarrolla en muchas instancias, de ahí que se hable de un punto de vista dentro de una argumentación, una marca pequeña y generalmente circular sobre algún material, un signo de puntuación que indica pausa en la lectura, unidad de medición en la mayoría de los deportes y juegos, y en la geografía indica un lugar. La definición: sucesión infinita de puntos en una sola dirección corresponde a: A.      Circulo B.      Punto C.      Vértice D.     Recta      13.  Teniendo en cuenta la definición anterior, y entendiendo que dimensión es la medida de las cosas según su forma y nuestra visión de ellas, por ejemplo, el volumen de un cuerpo, el área de una superficie o lo largo de una línea. ¿Cuántas dimensiones tiene una recta? A.      Tres B.      Dos C.      Una D.     Ninguna       14.  Un plano podemos definirlo como el lugar ideal en el cual existen infinito número de puntos y de rectas. Así como se puede pensar que al desplazar un punto en una sola dirección se obtiene una recta, también podemos decir que si desplazamos una recta en una sola dirección se obtiene un plano. Entonces, ¿Cuántas dimensiones tiene un plano? A.      Tres B.      Dos C.      Una D.     Ninguna     15.  Si tomamos un plano y lo movemos en una dirección obtenemos un espacio. ¿Cuántas dimensiones tiene un espacio? A.      Tres B.      Dos C.      Una D.     Ninguna       16.  Si se hace girar un punto sobre un plano siempre a la misma distancia de otro punto central al giro, se obtiene: A.      Una circunferencia B.      Una curva C.      Un circulo D.     Un ángulo       17.  Si fijamos el punto extremo de una recta en un plano y la hacemos girar sobre dicho punto, se obtiene: A.      Una curva B.      Una circunferencia C.      Un ángulo D.     Un circulo    18.  La circunferencia y el círculo tienen 360° grados cada uno. ¿Cuál de las siguientes características de esas dos figuras geométricas está equivocada? A.      El circulo posee dos dimensiones B.      La circunferencia tiene una dimensión C.      La circunferencia limita al circulo D.     El circulo tiene por unidad los metros lineales      19.  Los triángulos son polígonos de tres lados que cumplen con una regla o teorema, llamada Desigualdad Triangular, que básicamente dice: que la suma de dos lados de un triángulo siempre será mayor al lado restante o tercero. Dado este enunciado, escoja en las siguientes listas de longitudes de los lados triángulos, cual no cumple la desigualdad triangular. A.      30, 40 y 50 B.      70, 90, 10 C.      25, 35, 45 D.      82, 57, 40       20.  Nuestros campesinos colombianos hacen uso de una estrategia geométrica muy eficiente para medir la distancia de una vía, por ejemplo, el camino de la vereda hasta la carretera principal. Hacen una señal con pintura sobre la llanta delantera, que quede bastante visible para el conductor y hacen el recorrido que se quiere medir. ¿Qué elementos se deben tener en cuenta para hallar la medida de esa distancia? A.      El tiempo del recorrido y la velocidad media del mismo B.      Longitud de la circunferencia de la llanta y las vueltas dadas por ella C.      El número de vueltas en subida, bajada y en lo plano D.     El peso del conductor y la presión de las llantas

MOMENTO DE DESARROLLO

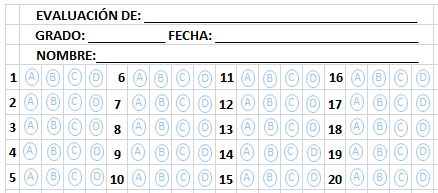
ACTIVIDAD/ES ESPECIFICAS/S ACCIONES A DESARROLLAR: Resolver las preguntas y dar su respuesta en la tabla de respuestas que encuentras al final de esta guía.

RECOMENDACIONES 1.      Leer y entender cada una de las preguntas de la presente guía. 2.      Tomar el tiempo necesario para cada pregunta. 3.      Utilizar la tabla de respuestas tipo Prueba Saber para indicar su decisión en cada pregunta.

MOMENTO FINAL

EVIDENCIA DE APRENDIZAJE (Explicación, descripción, graficas, representación u otra) RESULTADO A ENTREGAR: Enviar una imagen de su tabla de respuestas.

 “Quédate en casa…pronto nos volveremos a ver”